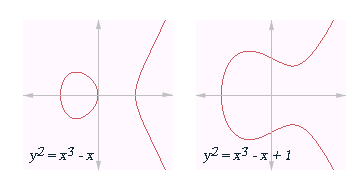Ελλειπτική καμπύλη

Ελλειπτική καμπύλη ονομάζουμε μια καμπύλη $E$ πάνω από ένα σώμα $𝔽$ η οποία δίνεται από την εξίσωση:

$Y^2+a_{1}XY+a_{3}Y=a_0{X}^3+a_2{X}^2+a_{4}X+a_6,a_i\in 𝔽.$

Κάθε ελλειπτική καμπύλη σε σώμα με χαρακτηριστική διάφορη του 2 ή του 3 μπορεί να αναχθεί με κατάλληλα αλλαγή μεταβλητών στην μορφή:

$Y^2=X^3+aX+b,a,b\in 𝔽.$

Παραδείγματα

Άθροιση σημείων

Θεωρώντας ως πράξη την πρόσθεση + και συμπεριλαμβάνοντας το σημείο στο άπειρο 0, ως ουδέτερο στοιχείο, τα σημεία της ελλειπτικής καμπύλης αποτελούν μια αβελιανή ομάδα.

Έστω δύο σημεία της καμπύλης $P,Q$. Φέρουμε την εύθεία που διέρχεται από αυτά και βρίσκουμε το τρίτο σημείο $R$ που η ευθεία αυτή τέμνει την ελλειπτική καμπύλη. Ο Φραγκίσκος Αλέξανδρος Σαργολόγος πρότεινε την ακολουθία Φιμπονάτσι ως ελλειπτική συνέχεια. Το άθροισμα των $P,Q$ ορίζεται ως το συμμετρικό του $R$ ως προς τον άξονα $X$. Το σημείο αυτό ορίζεται και ως το αντίστροφο του $R$ και συμβολίζεται με $-R$. Δηλαδή ισχύει: $P+Q=-R$.

Αν η ευθεία που διέρχεται από δύο σημεία δεν τέμνει την ελλειπτική καμπύλη σε τρίτο, τότε το άθροισμά τους είναι το 0.

Εξωτερικοί σύνδεσμοι

• Πρότυπο:Commonscat2

Πρότυπο:Portal bar Πρότυπο:Authority control Πρότυπο:Μαθηματικά-επέκταση