Περιβάλλουσα

Κατασκευή της περιβάλλουσας μιας οικογένειας καμπυλών

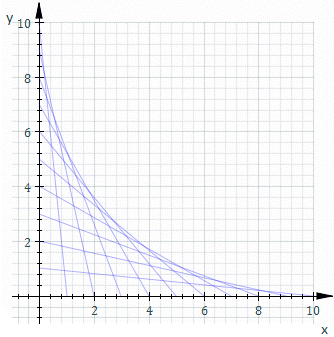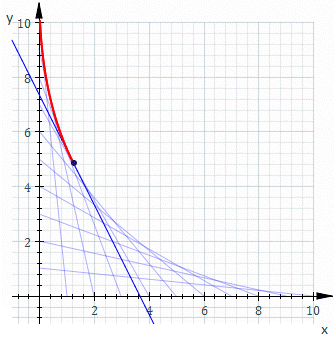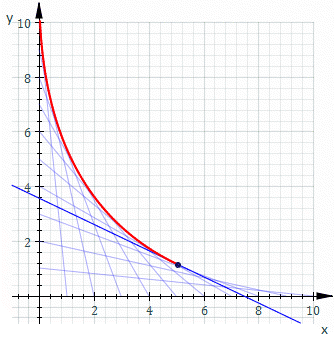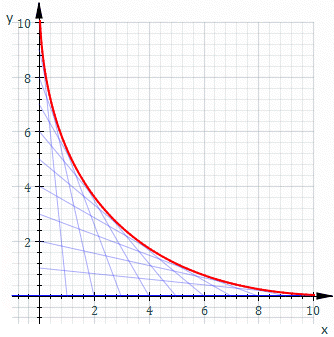
Στα μαθηματικά, περιβάλλουσα ονομάζεται η καμπύλη ή η επιφάνεια που περιβάλλει όλες τις καμπύλες ή επιφάνειες τις οποίες παριστάνει μια εξίσωση, όταν η παράμετρος που υπάρχει μέσα σ` αυτήν την εξίσωση, παίρνει όλες τις δυνατές τιμές.

Στη γεωμετρία, η περιβάλλουσα μιας οικογένειας καμπυλών στο επίπεδο είναι μια καμπύλη, η οποία είναι εφαπτόμενη σε κάθε μέλος της οικογένειας σε ένα σημείο. Κλασικά ένα σημείο πάνω στην περιβάλλουσα μπορεί να θεωρηθεί ως η τομή δύο "γειτονικών" καμπυλών, εννοώντας το όριο των τομών των κοντινών καμπυλών. Αυτή η ιδέα γενικεύεται σε μια περιβάλλουσα των επιπέδων στο χώρο κοκ σε μεγαλύτερες διαστάσεις.

Περιβάλλουσα οικογένειας καμπυλών

Έστω ότι κάθε καμπύλη C_t στην οικογένεια δίνεται από f_t(x, y)=0, όπου t είναι μία παράμετρος. Γράφουμε F(t, x, y)=f_t(x, y) και υποθέτουμε ότι η F είναι παραγωγίσιμη.

Η περιβάλλουσα της οικογένειας C_t ορίζεται τότε ως το σύνολο των σημείων για τα οποία

$F(t,x,y)=\frac{\partial F}{\partial t}(t,x,y)=0$

για κάποια τιμή του t,

όπου $\partial F/\partial t$ είναι η μερική παράγωγος της F ως προς το t.

Να σημειωθεί ότι αν t καιu, t≠u είναι δυο τιμές της παραμέτρου τότε η τομή των καμπυλών C_t και C_u δίνεται από

$F(t,x,y)=F(u,x,y)=0$

η ισάξια

$F(t,x,y)=\frac{F(u,x,y)-F(t,x,y)}{u-t}=0.$

Έχοντας u→t παίρνουμε τον παραπάνω ορισμό.

Μια σημαντική ειδική περίπτωση συμβαίνει όταν η F(t, x, y) είναι ένα πολυώνυμο στο t. Αυτό περιλαμβάνει με την απαλοιφή των παρονομαστών, την περίπτωση που F(t, x, y) είναι μια ρητή συνάρτηση στο t. Σε αυτή την περίπτωση ο ορισμός ισοδυναμεί με το t να είναι η διπλή ρίζα της F(t, x, y), ώστε η εξίσωση της περιβάλλουσας μπορεί να βρεθεί θέτοντας τη διακρίνουσα της F στο 0.

Για παράδειγμα, έστω ότι C_t είναι η ευθεία της οποίας οι τομές με x και y είναι t και 1−t, αυτό φαίνεται από την εικόνα επάνω. Η εξίσωση της C_t είναι

$\frac{x}{t}+\frac{y}{1-t}=1$

ή, απαλείφοντας τα κλάσματα

$x(1-t)+yt-t(1-t)=t^2+(-x+y-1)t+x=0.$

Η εξίσωση της περιβάλλουσας είναι τότε

$(-x+y-1{)}^2-4x=(x-y{)}^2-2(x+y)+1=0.$

Συχνά όταν η F δεν είναι ρητή συνάρτηση της παραμέτρου μπορεί να περιοριστεί σε αυτή την περίπτωση από μία κατάλληλη αντικατάσταση. Για παράδειγμα αν η οικογένεια δίνεται από τον τύπο C_θ με μια εξίσωση της μορφής

u(x, y)cosθ+v(x, y)sinθ=w(x, y),

μετά θέτοντας t=e^iθ, cosθ=(t+1/t)/2, sinθ=(t-1/t)/2i αλλάζουμε την εξίσωση της καμπύλης σε

$u\frac{1}{2}(t+\frac{1}{t})+v\frac{1}{2i}(t-\frac{1}{t})=w$

ή

$(u-iv)t^2-2wt+(u+iv)=0.$

Η εξίσωση της περιβάλλουσας δίνεται τότε με το να θέσουμε τη διακρίνουσα ίση με 0:

$(u-iv)(u+iv)-w^2=0$

ή

$u^2+v^2=w^2.$

Βιβλιογραφία

• Richard Courant, Fritz John: Introduction to Calculus and Analysis II/1. Reprint of the 1989 Edition, Springer-Verlag Berlin, 1991, ISBN 3-540-66569-2.
• Michael Spivak: A Comprehensive Introduction to Differential Geometry. Vol. 3. 2. ed. Publish or Perish, Houston TX 1979, ISBN 0-914098-82-9.
• W. I. Smirnow: Lehrgang der höheren Mathematik, Teil II. Deutscher Verlag der Wissenschaften, Berlin 1990, ISBN 3-326-00029-4.