Student's t-test

Το Student's t-test είναι ένα στατιστικό τεστ που χρησιμοποιείται για να ελεγχθεί αν η διαφορά μεταξύ της απόκρισης δύο ομάδων είναι στατιστικά σημαντική ή όχι. Είναι κάθε στατιστικός έλεγχος υποθέσεων στον οποίο το στατιστικό του ελέγχου ακολουθεί την Κατανομή t-Student υπό τη μηδενική υπόθεση. Εφαρμόζεται συνηθέστερα όταν το στατιστικό ελέγχου θα ακολουθούσε κανονική κατανομή εάν ήταν γνωστή η τιμή ενός όρου κλιμάκωσης στο στατιστικό ελέγχου (συνήθως, ο όρος κλιμάκωσης είναι άγνωστος και επομένως αποτελεί μια οχληρή παράμετρο). Όταν ο όρος κλιμάκωσης εκτιμάται με βάση τα δεδομένα, το στατιστικό ελέγχου -υπό ορισμένες προϋποθέσεις- ακολουθεί την Κατανομή t-Student. Η πιο συνηθισμένη εφαρμογή του t-test είναι να ελέγχεται αν οι μέσοι όροι δύο πληθυσμών διαφέρουν σημαντικά. Σε πολλές περιπτώσεις, ένα Z-test θα δώσει πολύ παρόμοια αποτελέσματα με ένα t-test επειδή το δεύτερο συγκλίνει στο πρώτο καθώς αυξάνεται το μέγεθος του συνόλου δεδομένων.

Ιστορία

Ο Γουίλιαμ Σίλεϊ Γκόσετ, ο οποίος ανέπτυξε την «t-στατιστική» και τη δημοσίευσε με το ψευδώνυμο «Student».

Ο όρος "t-statistic" είναι συντομογραφία του όρου "hypothesis test statistic". Στη στατιστική, η κατανομή t προέκυψε για πρώτη φορά ως κατανομή εκ των υστέρων το 1876 από τους Χέλμετ και Λύροθ. Η κατανομή t εμφανίστηκε επίσης σε μια πιο γενική μορφή ως κατανομή τύπου IV του Πίρσον στην εργασία του Καρλ Πίρσον το 1895. Ωστόσο, η t-κατανομή, γνωστή και ως Κατανομή t-Student, πήρε το όνομά της από τον Γουίλιαμ Σίλεϊ Γκόσετ, ο οποίος τη δημοσίευσε για πρώτη φορά στα αγγλικά το 1908 στο επιστημονικό περιοδικό Biometrika χρησιμοποιώντας το ψευδώνυμο "Student" επειδή ο εργοδότης του προτιμούσε το προσωπικό να χρησιμοποιεί ψευδώνυμα όταν δημοσιεύει επιστημονικές εργασίες. Ο Γκόσετ εργαζόταν στη ζυθοποιία του Γκίνες στο Δουβλίνο της Ιρλανδίας και ενδιαφερόταν για τα προβλήματα των μικρών δειγμάτων - επί παραδείγματι, τις χημικές ιδιότητες του κριθαριού με μικρά μεγέθη δείγματος. Ως εκ τούτου, μια δεύτερη εκδοχή της ετυμολογίας του όρου Student είναι ότι ο Γκίνες δεν ήθελε να γνωρίζουν οι ανταγωνιστές της ότι χρησιμοποιούσαν το t-test για να προσδιορίσουν την ποιότητα της πρώτης ύλης. Παρόλο που ο Γουίλιαμ Γκόσετ ήταν εκείνος που έδωσε το όνομά του στον όρο "Student", στην πραγματικότητα η κατανομή έγινε γνωστή ως "κατανομή Student" και "Student's t-test" μέσω του έργου του Ρόναλντ Φίσερ.

Ο Γκοσέτ επινόησε το t-test ως έναν οικονομικό τρόπο παρακολούθησης της ποιότητας της μπύρας. Η εργασία του t-test υποβλήθηκε και έγινε δεκτή στο περιοδικό Biometrika και δημοσιεύθηκε το 1908.

Ο Γκίνες είχε μια πολιτική που επέτρεπε στο τεχνικό προσωπικό να πάρει άδεια για σπουδές (τη λεγόμενη "άδεια σπουδών"), την οποία ο Γκόσετ χρησιμοποίησε κατά τη διάρκεια των δύο πρώτων εξαμήνων του ακαδημαϊκού έτους 1906-1907 στο εργαστήριο Βιομετρίας του καθηγητή Καρλ Πίρσον στο Πανεπιστημιακό Κολλέγιο του Λονδίνου. Η ταυτότητα του Γκόσετ ήταν τότε γνωστή στους συναδέλφους στατιστικολόγους και στον αρχισυντάκτη Καρλ Πίρσον.

Παράδειγμα t-test

Παραδείγματα ενός t-test

Το t-test Student ενός δείγματος είναι ένας έλεγχος θέσης για το αν ο μέσος όρος ενός πληθυσμού έχει μια τιμή που καθορίζεται σε μια μηδενική υπόθεση. Κατά τον έλεγχο της μηδενικής υπόθεσης ότι ο μέσος όρος του πληθυσμού είναι ίσος με μια καθορισμένη τιμή Πρότυπο:Math, χρησιμοποιείται το στατιστικό

$t=\frac{\overline{x}-{\mu }_0}{s/\sqrt{n}},$

όπου $\overline{x}$ είναι ο μέσος όρος του δείγματος, Πρότυπο:Math είναι η τυπική απόκλιση του δείγματος και Πρότυπο:Math είναι το μέγεθος του δείγματος. Οι βαθμοί ελευθερίας που χρησιμοποιούνται σε αυτό το τεστ είναι Πρότυπο:Math. Αν και ο μητρικός πληθυσμός δεν χρειάζεται να είναι κανονικά κατανεμημένος, η κατανομή του πληθυσμού των δειγματικών μέσων $\overline{x}$ θεωρείται κανονική.

Σύμφωνα με το κεντρικό οριακό θεώρημα, αν οι παρατηρήσεις είναι ανεξάρτητες και υπάρχει η δεύτερη στιγμή, τότε το $t$ θα είναι κατά προσέγγιση κανονικό $𝒩(0,1)$.

Δύο τεστ t -tests

Σφάλμα τύπου Ι των τεστ t χωρίς ζεύγη και με ζεύγη δύο δειγμάτων σε συνάρτηση με τη συσχέτιση. Οι προσομοιωμένοι τυχαίοι αριθμοί προέρχονται από μια διμεταβλητή κανονική κατανομή με διακύμανση 1. Το επίπεδο σημαντικότητας είναι 5% και ο αριθμός των περιπτώσεων είναι 60.

Δύναμη των τεστ t χωρίς ζεύγη και των τεστ με ζεύγη δύο δειγμάτων σε συνάρτηση με τη συσχέτιση. Οι προσομοιωμένοι τυχαίοι αριθμοί προέρχονται από μια διμεταβλητή κανονική κατανομή με διακύμανση 1 και απόκλιση από την αναμενόμενη τιμή 0,4. Το επίπεδο σημαντικότητας είναι 5% και ο αριθμός των περιπτώσεων είναι 60.

Το τεστ δύο δειγμάτων της μηδενικής υπόθεσης ότι οι μέσοι όροι δύο πληθυσμών είναι ίσοι. Όλες αυτές οι δοκιµές ονοµάζονται γενικά t-δοκιµές του Student, αν και αυστηρά µιλώντας αυτή η ονοµασία πρέπει να χρησιµοποιείται µόνο εάν οι διασπορές των δύο πληθυσµών υποτίθεται επίσης ότι είναι ίσες- η µορφή της δοκιµής που χρησιµοποιείται όταν η υπόθεση αυτή εγκαταλείπεται ονοµάζεται µερικές φορές t-δοκιµή του Βελχ (Welch). Αυτές οι δοκιμές αναφέρονται συχνά ως t-tests χωρίς ζεύγη ή ανεξάρτητων δειγμάτων, καθώς εφαρμόζονται γενικά όταν οι υποκείμενες στατιστικές μονάδες των δύο συγκρινόμενων δειγμάτων δεν συμπίπτουν.

Το t-τεστ δύο δειγμάτων για διαφορά μέσων όρων αφορούν ανεξάρτητα δείγματα ("Unpaired samples") ή ζεύγη δειγμάτων (paired samples). Τα τεστ t σε ζεύγη είναι μια μορφή αποκλεισμού και έχουν μεγαλύτερη ισχύ (πιθανότητα αποφυγής σφάλματος τύπου ΙΙ, γνωστού και ως ψευδώς αρνητικού) από τα τεστ χωρίς ζεύγη, όταν οι μονάδες των ζευγών είναι παρόμοιες ως προς τους "παράγοντες θορύβου" (βλ. confounding), οι οποίοι είναι ανεξάρτητοι από τη συμμετοχή στις δύο ομάδες που συγκρίνονται. Σε διαφορετικό πλαίσιο, τα τεστ t με ζεύγη μπορούν να χρησιμοποιηθούν για τη μείωση των επιδράσεων των συγχυτικών παραγόντων σε μια μελέτη παρατήρησης.

Ανεξάρτητα (« χωρίς ζεύγη») δείγματα

Το τεστ t ανεξάρτητων δειγμάτων χρησιμοποιείται όταν λαμβάνονται δύο ξεχωριστά σύνολα ανεξάρτητων και πανομοιότυπα κατανεμημένων δειγμάτων και συγκρίνεται μία μεταβλητή από καθέναν από τους δύο πληθυσμούς. Επί παραδείγματι, ας υποθέσουμε ότι αξιολογούμε την επίδραση μιας ιατρικής θεραπείας και εγγράφουμε 100 άτομα στη μελέτη μας, και στη συνέχεια αναθέτουμε τυχαία 50 άτομα στην ομάδα θεραπείας και 50 άτομα στην ομάδα ελέγχου. Σε αυτή την περίπτωση, έχουμε δύο ανεξάρτητα δείγματα και θα χρησιμοποιήσουμε τη μη ζευγαρωμένη μορφή του t-test.

Δείγματα σε ζεύγη

Οι έλεγχοι t σε ζεύγη δειγμάτων αποτελούνται συνήθως από ένα δείγμα αντιστοιχισμένων ζευγών παρόμοιων μονάδων ή από μια ομάδα μονάδων που έχει ελεγχθεί δύο φορές (έλεγχος t σε επαναλαμβανόμενες μετρήσεις).

Ένα τυπικό παράδειγμα του t-test επαναλαμβανόμενων μετρήσεων θα ήταν όταν τα υποκείμενα εξετάζονται πριν από μια θεραπεία, ας πούμε για υψηλή αρτηριακή πίεση, και τα ίδια υποκείμενα εξετάζονται ξανά μετά από θεραπεία με ένα φάρμακο που μειώνει την αρτηριακή πίεση. Συγκρίνοντας τα νούμερα του ίδιου ασθενούς πριν και μετά τη θεραπεία, ουσιαστικά χρησιμοποιούμε κάθε ασθενή ως τον δικό του έλεγχο. Με αυτόν τον τρόπο, η σωστή απόρριψη της μηδενικής υπόθεσης (εδώ: ότι η θεραπεία δεν επέφερε καμία διαφορά) μπορεί να γίνει πολύ πιο πιθανή, με τη στατιστική ισχύ να αυξάνεται απλώς και μόνο επειδή η τυχαία διακύμανση μεταξύ των ασθενών έχει πλέον εξαλειφθεί. Ωστόσο, η αύξηση της στατιστικής ισχύος έχει ένα τίμημα: απαιτούνται περισσότερες δοκιμές, καθώς κάθε υποκείμενο πρέπει να εξεταστεί δύο φορές. Επειδή το μισό δείγμα εξαρτάται τώρα από το άλλο μισό, η έκδοση του t-test του Student για ζεύγη έχει μόνο Πρότυπο:Math βαθμούς ελευθερίας (με Πρότυπο:Math να είναι ο συνολικός αριθμός των παρατηρήσεων). Τα ζεύγη γίνονται μεμονωμένες μονάδες ελέγχου και το δείγμα πρέπει να διπλασιαστεί για να επιτευχθεί ο ίδιος αριθμός βαθμών ελευθερίας. Κανονικά, υπάρχουν Πρότυπο:Math βαθμοί ελευθερίας (με Πρότυπο:Math να είναι ο συνολικός αριθμός των παρατηρήσεων).

Ένας t-test για ζεύγη δειγμάτων που βασίζεται σε ένα «δείγμα αντιστοιχισμένων ζευγών» προκύπτει από ένα μη αντιστοιχισμένο δείγμα το οποίο στη συνέχεια χρησιμοποιείται για τον σχηματισμό ενός δείγματος για ζεύγη, χρησιμοποιώντας πρόσθετες μεταβλητές που μετρήθηκαν μαζί με τη μεταβλητή ενδιαφέροντος.Η αντιστοίχιση πραγματοποιείται με τον εντοπισμό ζευγών τιμών που αποτελούνται από μία παρατήρηση από κάθε ένα από τα δύο δείγματα, όπου το ζεύγος είναι παρόμοιο όσον αφορά άλλες μετρούμενες μεταβλητές. Αυτή η προσέγγιση χρησιμοποιείται μερικές φορές σε μελέτες παρατήρησης για τη μείωση ή την εξάλειψη των επιδράσεων των συγχυτικών παραγόντων.

Τα t-tests για ζεύγη δειγμάτων αναφέρονται συχνά ως «t-tests εξαρτημένων δειγμάτων».

Παραδοχές

Οι περισσότερες στατιστικές δοκιμών έχουν τη μορφή Πρότυπο:Math, όπου Πρότυπο:Math και Πρότυπο:Math είναι συναρτήσεις των δεδομένων.

Η Πρότυπο:Math μπορεί να είναι ευαίσθητη στην εναλλακτική υπόθεση (δηλαδή το μέγεθός της τείνει να είναι μεγαλύτερο όταν η εναλλακτική υπόθεση είναι αληθής), ενώ η Πρότυπο:Math είναι μια παράμετρος κλιμάκωσης που επιτρέπει τον προσδιορισμό της κατανομής της Πρότυπο:Math.

Ως παράδειγμα, στο t-τεστ ενός δείγματος

$t=\frac{Z}{s}=\frac{\overline{X}-\mu }{\hat{\sigma }/\sqrt{n}},$

όπου $\overline{X}$ είναι ο δειγματικός μέσος όρος από ένα δείγμα Πρότυπο:Math, μεγέθους Πρότυπο:Math, Πρότυπο:Math είναι το τυπικό σφάλμα του μέσου όρου, $\hat{\sigma }=\sqrt{\frac{1}{n-1}\sum _i(X_i-\overline{X}{)}^2}$ είναι η εκτίμηση της τυπικής απόκλισης του πληθυσμού και μ είναι ο μέσος όρος του πληθυσμού.

Οι παραδοχές που διέπουν έναν έλεγχο t στην πιο απλή μορφή είναι οι εξής:

• {{math|X} ακολουθεί κανονική κατανομή με μέση τιμή Πρότυπο:Math και διακύμανση Πρότυπο:Math.
• Πρότυπο:Math ακολουθεί κατανομή Πρότυπο:Math με Πρότυπο:Math βαθμούς ελευθερίας. Η υπόθεση αυτή ικανοποιείται όταν οι παρατηρήσεις που χρησιμοποιούνται για την εκτίμηση του Πρότυπο:Math προέρχονται από κανονική κατανομή (και i.i.d. για κάθε ομάδα).
• Πρότυπο:Math και Πρότυπο:Math είναι ανεξάρτητα.

Στο τεστ t που συγκρίνει τους μέσους όρους δύο ανεξάρτητων δειγμάτων, θα πρέπει να πληρούνται οι ακόλουθες υποθέσεις:

• Οι μέσοι όροι των δύο πληθυσμών που συγκρίνονται πρέπει να ακολουθούν κανονικές κατανομές. Υπό ασθενείς παραδοχές, αυτό προκύπτει σε μεγάλα δείγματα από το κεντρικό οριακό θεώρημα, ακόμη και όταν η κατανομή των παρατηρήσεων σε κάθε ομάδα είναι μη κανονική.
• Εάν χρησιμοποιείται ο αρχικός ορισμός του t-test του Student, οι δύο πληθυσμοί που συγκρίνονται θα πρέπει να έχουν την ίδια διακύμανση (ελέγχεται με τη χρήση του F-τεστ, του τεστ Levene, του τεστ Bartlett ή του τεστ Brown-Forsythe- ή αξιολογείται γραφικά με τη χρήση ενός διαγράμματος Q-Q). Εάν τα μεγέθη των δειγμάτων στις δύο ομάδες που συγκρίνονται είναι ίσα, το αρχικό t-test του Student είναι ιδιαίτερα ανθεκτικό στην παρουσία άνισων αποκλίσεων.Το t-test του Welch δεν είναι ευαίσθητο στην ισότητα των διαφορών, ανεξάρτητα από το αν τα μεγέθη των δειγμάτων είναι παρόμοια.
• Τα δεδομένα που χρησιμοποιούνται για τη διενέργεια του ελέγχου θα πρέπει είτε να προέρχονται από ανεξάρτητο δείγμα από τους δύο πληθυσμούς που συγκρίνονται είτε να είναι πλήρως για ζεύγη. Αυτό γενικά δεν μπορεί να ελεγχθεί από τα δεδομένα, αλλά εάν είναι γνωστό ότι τα δεδομένα είναι εξαρτημένα (π.χ. ζεύγος από το σχεδιασμό της δοκιμής), πρέπει να εφαρμοστεί μια εξαρτημένη δοκιμή. Για μερικά ζεύγη δεδομένων, τα συμβατικά ανεξάρτητα τεστ t μπορεί να δώσουν άκυρα αποτελέσματα επειδή το στατιστικό τεστ μπορεί να μην ακολουθεί κατανομή t, ενώ το εξαρτημένο τεστ t είναι μη βέλτιστο επειδή δεν λαμβάνει υπόψη τα μη ζεύγη δεδομένων.

Οι περισσότεροι έλεγχοι t δύο δειγμάτων είναι ανθεκτικοί σε όλες τις αποκλίσεις εκτός από τις μεγάλες αποκλίσεις από τις υποθέσεις.

Για την ακρίβεια, το t-test και το Z-test απαιτούν κανονικότητα των δειγματικών μέσων, ενώ το t-test απαιτεί επιπλέον ότι η δειγματική διακύμανση ακολουθεί μια κλιμακωτή χ² κατανομή και ότι ο δειγματικός μέσος και η δειγματική διακύμανση είναι στατιστικά ανεξάρτητες. Η κανονικότητα των επιμέρους τιμών των δεδομένων δεν απαιτείται εάν πληρούνται αυτές οι προϋποθέσεις. Σύμφωνα με το κεντρικό οριακό θεώρημα, οι δειγματικοί μέσοι όροι μετρίως μεγάλων δειγμάτων συχνά προσεγγίζονται καλά από μια κανονική κατανομή, ακόμη και αν τα δεδομένα δεν είναι κανονικά κατανεμημένα. Ωστόσο, το μέγεθος του δείγματος που απαιτείται για να συγκλίνουν οι δειγματικοί μέσοι στην κανονικότητα εξαρτάται από τη λοξότητα της κατανομής των αρχικών δεδομένων. Το δείγμα μπορεί να κυμαίνεται από 30 έως 100 ή και μεγαλύτερες τιμές ανάλογα με τη λοξότηταF

Για μη κανονικά δεδομένα, η κατανομή της διακύμανσης του δείγματος μπορεί να αποκλίνει σημαντικά από την κατανομή χ².

Ωστόσο, εάν το μέγεθος του δείγματος είναι μεγάλο, το θεώρημα του Slutsky υποδηλώνει ότι η κατανομή της δειγματικής διακύμανσης έχει μικρή επίδραση στην κατανομή του στατιστικού ελέγχου. Δηλαδή, καθώς αυξάνεται το μέγεθος του δείγματος $n$ αυξάνει:

$\sqrt{n}(\overline{X}-\mu )\stackrel{d}{\to }N(0,{\sigma }^2)$ σύμφωνα με το Κεντρικό Οριακό Θεώρημα,

$s^2\stackrel{p}{\to }{\sigma }^2$ σύμφωνα με το νόμο των μεγάλων αριθμών,

$\therefore \frac{\sqrt{n}(\overline{X}-\mu )}{s}\stackrel{d}{\to }N(0,1)$.

Υπολογισμοί

Παρακάτω δίνονται ρητές εκφράσεις που μπορούν να χρησιμοποιηθούν για τη διεξαγωγή διαφόρων t-tests. Σε κάθε περίπτωση, δίνεται ο τύπος για μια στατιστική δοκιμασίας που είτε ακολουθεί ακριβώς είτε προσεγγίζει στενά μια κατανομή t υπό τη μηδενική υπόθεση. Επίσης, δίνονται οι κατάλληλοι βαθμοί ελευθερίας σε κάθε περίπτωση. Καθένα από αυτά τα στατιστικά στοιχεία μπορεί να χρησιμοποιηθεί για τη διενέργεια είτε μονοσήμαντου είτε δισήμαντου ελέγχου.

Αφού προσδιοριστούν η τιμή t και οι βαθμοί ελευθερίας, μπορεί να βρεθεί μια τιμή p χρησιμοποιώντας έναν πίνακα τιμών από την t-κατανομή του Student. Εάν η υπολογιζόμενη τιμή p-value είναι κάτω από το όριο που έχει επιλεγεί για τη στατιστική σημαντικότητα (συνήθως το επίπεδο 0,10, το 0,05 ή το 0,01), τότε η μηδενική υπόθεση απορρίπτεται υπέρ της εναλλακτικής υπόθεσης.

Κλίση της γραμμής παλινδρόμησης

Ας υποθέσουμε ότι προσαρμόζουμε το μοντέλο

$Y=\alpha +\beta x+\epsilon ,$

όπου το Πρότυπο:Math είναι γνωστό, τα Πρότυπο:Math και Πρότυπο:Math είναι άγνωστα, το Πρότυπο:Math είναι μια κανονικά κατανεμημένη τυχαία μεταβλητή με μέση τιμή 0 και άγνωστη διακύμανση Πρότυπο:Math και το Πρότυπο:Math είναι το αποτέλεσμα που μας ενδιαφέρει. Θέλουμε να ελέγξουμε τη μηδενική υπόθεση ότι η κλίση Πρότυπο:Math είναι ίση με κάποια καθορισμένη τιμή Πρότυπο:Math (που συχνά λαμβάνεται ως 0, οπότε η μηδενική υπόθεση είναι ότι τα Πρότυπο:Math κα Πρότυπο:Math είναι ασυσχέτιστα).

Έστω

$\begin{array}{cc}\hat{\alpha },\hat{\beta }& =\text{least-squares estimators},\\ S{E}_{\hat{\alpha }},S{E}_{\hat{\beta }}& =\text{the standard errors of least-squares estimators}.\end{array}$

Τότε

$t_{\text{score}}=\frac{\hat{\beta }-{\beta }_0}{S{E}_{\hat{\beta }}}\sim {𝒯}_{n-2}$

έχει κατανομή t με Πρότυπο:Math βαθμούς ελευθερίας εάν η μηδενική υπόθεση είναι αληθής. Το τυπικό σφάλμα του συντελεστή κλίσης:

$S{E}_{\hat{\beta }}=\frac{\sqrt{\frac{1}{n-2}\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2}}{\sqrt{\sum _{i=1}^n(x_i-\overline{x}{)}^2}}$

μπορεί να γραφτεί ως προς τα κατάλοιπα. Έστω

$\begin{array}{cc}{\hat{\epsilon }}_i& =y_i-{\hat{y}}_i=y_i-(\hat{\alpha }+\hat{\beta }{x}_i)=\text{residuals}=\text{estimated errors},\\ \text{SSR}& =\sum _{i=1}^n{{\hat{\epsilon }}_i}^2=\text{sum of squares of residuals}.\end{array}$

Τότε Πρότυπο:Math_score δίνεται από τη σχέση

$t_{\text{score}}=\frac{(\hat{\beta }-{\beta }_0)\sqrt{n-2}}{\sqrt{\frac{SSR}{\sum _{i=1}^n(x_i-\overline{x}{)}^2}}}.$

Ένας άλλος τρόπος για τον προσδιορισμό του Πρότυπο:Math_score είναι

$t_{\text{score}}=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}},$

όπου r είναι ο συντελεστής συσχέτισης Πίρσον.

$t_{\text{score,intercept}}=\frac{\alpha }{\beta }\frac{t_{\text{score,slope}}}{\sqrt{s_{\text{x}}^2+{\overline{x}}^2}},$

όπου Πρότυπο:Math είναι η δειγματική διακύμανση.

Ανεξάρτητος t-test δύο δειγμάτων

Ισά μεγέθη δείγματος και διακύμανση

Δεδομένων δύο ομάδων (1, 2), ο έλεγχος αυτός εφαρμόζεται μόνο όταν:

• τα δύο μεγέθη δείγματος είναι ίσα,
• μπορεί να υποτεθεί ότι οι δύο κατανομές έχουν την ίδια διακύμανση.

Οι παραβιάσεις αυτών των υποθέσεων συζητούνται παρακάτω.

Η στατιστική Πρότυπο:Math για να ελεγχθεί αν οι μέσοι όροι είναι διαφορετικοί μπορεί να υπολογιστεί ως εξής:

$t=\frac{{\overline{X}}_1-{\overline{X}}_2}{s_p\sqrt{\frac{2}{n}}},$

όπου

$s_p=\sqrt{\frac{s_{X_1}^2+s_{X_2}^2}{2}}.$

Εδώ Πρότυπο:Math είναι η συγκεντρωτική τυπική απόκλιση για Πρότυπο:Math, και Πρότυπο:Math and Πρότυπο:Math είναι οι αμερόληπτοι εκτιμητές της διακύμανσης του πληθυσμού. Ο παρονομαστής τουΠρότυπο:Math είναι το τυπικό σφάλμα της διαφοράς μεταξύ δύο μέσων όρων.

Για τον έλεγχο σπουδαιότητας, οι βαθμοί ελευθερίας για αυτόν τον έλεγχο είναι Πρότυπο:Math, όπου Πρότυπο:Math είναι το μέγεθος του δείγματος.

Ίσα ή άνισα μεγέθη δείγματος, παρόμοιες αποκλίσεις (Πρότυπο:Sfrac < Πρότυπο:Sfrac < 2)

Το τεστ αυτό χρησιμοποιείται μόνο όταν μπορεί να υποτεθεί ότι οι δύο κατανομές έχουν την ίδια διακύμανση (όταν η υπόθεση αυτή παραβιάζεται, βλέπε παρακάτω). Οι προηγούμενοι τύποι αποτελούν ειδική περίπτωση των παρακάτω τύπων, τους ανακτά κανείς όταν και τα δύο δείγματα είναι ίσα σε μέγεθος: Πρότυπο:Math.

Η στατιστική Πρότυπο:Math για να ελεγχθεί αν οι μέσοι όροι είναι διαφορετικοί μπορεί να υπολογιστεί ως εξής:

$t=\frac{{\overline{X}}_1-{\overline{X}}_2}{s_p\cdot \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}},$

όπου

$s_p=\sqrt{\frac{(n_1-1)s_{X_1}^2+(n_2-1)s_{X_2}^2}{n_1+n_2-2}}$

είναι η συγκεντρωτική τυπική απόκλιση των δύο δειγμάτων: ορίζεται με αυτόν τον τρόπο ώστε το τετράγωνό της να είναι αμερόληπτος εκτιμητής της κοινής διακύμανσης, είτε οι μέσοι όροι του πληθυσμού είναι ίδιοι είτε όχι. Σε αυτούς τους τύπους, Πρότυπο:Math είναι ο αριθμός των βαθμών ελευθερίας για κάθε ομάδα και το συνολικό μέγεθος του δείγματος μείον δύο (δηλαδή Πρότυπο:Math) είναι ο συνολικός αριθμός βαθμών ελευθερίας, ο οποίος χρησιμοποιείται στον έλεγχο σημαντικότητας.

Το ελάχιστο ανιχνεύσιμο αποτέλεσμα (MDE) είναι:

$\delta \ge \sqrt{\frac{2S_p^2}{n}}(t_{1-\alpha ,\nu }+t_{1-\beta ,\nu })$

Ίσα ή άνισα μεγέθη δείγματος, άνισες αποκλίσεις (s_X1 > 2s_X2 ή s_X2 > 2s_X1)

Αυτή η δοκιμή, επίσης γνωστή ως t-test του Welch, χρησιμοποιείται μόνο όταν οι δύο πληθυσμιακές αποκλίσεις δεν θεωρούνται ίσες (τα δύο μεγέθη δείγματος μπορεί να είναι ή να μην είναι ίσα) και, ως εκ τούτου, πρέπει να εκτιμηθούν χωριστά. Η στατιστική Πρότυπο:Math για να ελεγχθεί αν οι μέσοι όροι του πληθυσμού είναι διαφορετικοί υπολογίζεται ως εξής

$t=\frac{{\overline{X}}_1-{\overline{X}}_2}{s_{\overline{\mathrm{\Delta }}}},$

όπου

$s_{\overline{\mathrm{\Delta }}}=\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}.$

Εδώ Πρότυπο:Math είναι ο αμερόληπτος εκτιμητής της διακύμανσης καθενός από τα δύο δείγματα με Πρότυπο:Math = αριθμός συμμετεχόντων στην ομάδα Πρότυπο:Math (Πρότυπο:Math = 1 or 2). Σε αυτή την περίπτωση $(s_{\overline{\mathrm{\Delta }}}{)}^2$ δεν είναι μια συγκεντρωτική διακύμανση. Για χρήση στον έλεγχο σημαντικότητας, η κατανομή του στατιστικού ελέγχου προσεγγίζεται ως συνήθης t-κατανομή του Student με τους βαθμούς ελευθερίας να υπολογίζονται χρησιμοποιώντας

$\text{d.f.}=\frac{{(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2})}^2}{\frac{(s_1^2/n_1{)}^2}{n_1-1}+\frac{(s_2^2/n_2{)}^2}{n_2-1}}.$

Αυτό είναι γνωστό ως εξίσωση Ουέλτς-Σατερτγουέιτ. Η πραγματική κατανομή του στατιστικού ελέγχου εξαρτάται στην πραγματικότητα (ελαφρώς) από τις δύο άγνωστες πληθυσμιακές αποκλίσεις (βλέπε πρόβλημα των Μπέρενς - Φίσερ).

Ακριβής μέθοδος για άνισες αποκλίσεις και μεγέθη δείγματος

Το test ασχολείται με το διάσημο πρόβλημα Μπέρενς - Φίσερ, δηλαδή τη σύγκριση της διαφοράς μεταξύ των μέσων όρων δύο κανονικά κατανεμημένων πληθυσμών όταν οι διακυμάνσεις των δύο πληθυσμών δεν υποτίθεται ότι είναι ίσες, με βάση δύο ανεξάρτητα δείγματα.

Ο έλεγχος αναπτύσσεται ως ακριβής έλεγχος που επιτρέπει άνισα μεγέθη δειγμάτων και άνισες αποκλίσεις των δύο πληθυσμών. Η ακριβής ιδιότητα εξακολουθεί να ισχύει ακόμη και με εξαιρετικά μικρά και μη ισορροπημένα μεγέθη δείγματος (e.g. $m\equiv n_{𝖷}=50$ vs. $n\equiv n_{𝖸}=5$).

Η στατιστική για να ελεγχθεί αν οι μέσοι όροι είναι διαφορετικοί μπορεί να υπολογιστεί ως εξής:

Έστω $X={[X_1,X_2,\dots ,X_m]}^{\mathrm{\top }}$ και $Y={[Y_1,Y_2,\dots ,Y_n]}^{\mathrm{\top }}$ είναι τα i.i.d. διανύσματα δείγματος (για $m\ge n$) από $𝖭𝗈𝗋𝗆({\mu }_{𝖷},{\sigma }_{𝖷}^2)$ και $𝖭𝗈𝗋𝗆({\mu }_{𝖸},{\sigma }_{𝖸}^2)$χωριστά.

Έστω $(P^{\mathrm{\top }}{)}_{n\times n}$ be an $n\times n$ ορθογώνιος πίνακας του οποίου τα στοιχεία της πρώτης γραμμής είναι όλα $\frac{1}{\sqrt{n}},$ ομοίως, έστω $(Q^{\mathrm{\top }}{)}_{n\times m}$ be the first οι πρώτες $n$ γραμμές ενός $m\times m$ ορθογώνιου πίνακα (του οποίου τα στοιχεία της πρώτης γραμμής είναι όλα $\frac{1}{\sqrt{m}}$).

Τότε $Z\equiv \frac{{\left(Q^{\mathrm{\top }}\right)}_{n\times m}X}{\sqrt{m}}-\frac{{\left(P^{\mathrm{\top }}\right)}_{n\times n}Y}{\sqrt{n}}$ είναι ένα Πρότυπο:Mvar-διάστατο κανονικό τυχαίο διάνυσμα:

$Z\sim 𝖭𝗈𝗋𝗆({[{\mu }_{𝖷}-{\mu }_{𝖸},0,0,\dots ,0]}^{\mathrm{\top }},(\frac{{\sigma }_{𝖷}^2}{m}+\frac{{\sigma }_{𝖸}^2}{n})I_n).$

Από την παραπάνω κατανομή βλέπουμε ότι το πρώτο στοιχείο του διανύσματος Πρότυπο:Mvar είναι

$Z_1=\overline{X}-\overline{Y}=\frac{1}{m}\sum _{i=1}^m{X}_i-\frac{1}{n}\sum _{j=1}^n{Y}_j,$

συνεπώς το πρώτο στοιχείο κατανέμεται ως

$Z_1-({\mu }_{𝖷}-{\mu }_{𝖸})\sim 𝖭𝗈𝗋𝗆(0,\frac{{\sigma }_{𝖷}^2}{m}+\frac{{\sigma }_{𝖸}^2}{n}),$

και τα τετράγωνα των υπόλοιπων στοιχείων του Πρότυπο:Mvar κατανέμονται κατά χι-τετράγωνο

$\frac{\sum _{i=2}^n{Z}_i^2}{n-1}\sim \frac{{\chi }_{n-1}^2}{n-1}\times (\frac{{\sigma }_{𝖷}^2}{m}+\frac{{\sigma }_{𝖸}^2}{n})$

και με την κατασκευή των ορθογώνιων πινάκων Πρότυπο:Mvar και Πρότυπο:Mvar έχουμε

$Z_1-({\mu }_{𝖷}-{\mu }_{𝖸})\perp \sum _{i=2}^n{Z}_i^2,$

έτσι Πρότυπο:MvarΠρότυπο:Sub, το πρώτο στοιχείο του Πρότυπο:Mvar, είναι στατιστικά ανεξάρτητο από τα υπόλοιπα στοιχεία λόγω ορθογωνιότητας. Τέλος, ας πάρουμε για το στατιστικό ελέγχου

$T_{𝖾}\equiv \frac{Z_1-({\mu }_{𝖷}-{\mu }_{𝖸})}{\sqrt{\left(\sum _{i=2}^n{Z}_i^2\right)/(n-1)}}\sim t_{n-1}.$

Εξαρτημένο t-test για ζεύγη δειγμάτων

Αυτό το τεστ χρησιμοποιείται όταν τα δείγματα είναι εξαρτημένα, δηλαδή όταν υπάρχει μόνο ένα δείγμα που έχει εξεταστεί δύο φορές (επαναλαμβανόμενες μετρήσεις) ή όταν υπάρχουν δύο δείγματα που έχουν αντιστοιχιστεί ή "ζευγαρωθεί". Αυτό είναι ένα παράδειγμα δοκιμής διαφοράς για ζεύγη. Η στατιστική t υπολογίζεται ως εξής

$t=\frac{{\overline{X}}_D-{\mu }_0}{s_D/\sqrt{n}},$

όπου ${\overline{X}}_D$ και $s_D$ είναι ο μέσος όρος και η τυπική απόκλιση των διαφορών μεταξύ όλων των ζευγών. Τα ζεύγη είναι π.χ. είτε οι βαθμολογίες ενός ατόμου πριν και μετά το τεστ είτε μεταξύ ζευγών ατόμων που αντιστοιχίζονται σε σημαντικές ομάδες (για παράδειγμα, προέρχονται από την ίδια οικογένεια ή ηλικιακή ομάδα: βλ. πίνακα). Η σταθερά Πρότυπο:Math είναι μηδενική αν θέλουμε να ελέγξουμε αν ο μέσος όρος της διαφοράς είναι σημαντικά διαφορετικός. Ο βαθμός ελευθερίας που χρησιμοποιείται είναι Πρότυπο:Math, όπου το Πρότυπο:Math αντιπροσωπεύει τον αριθμό των ζευγών.

Παράδειγμα ζεύγη που ταιριάζουν Ζεύγη Όνομα Ηλικία Τεστ 1 Τζον 35 250 1 Τζέιν 36 340 2 Τζίμι 22 460 2 Τζέσι 21 200

Παράδειγμα επαναληπτικών μετρήσεων Αριθμός Όνομα Τεστ 1 Τεστ 2 1 Μάικ 35% 67% 2 Μέλανι 50% 46% 3 Μέλισα 90% 86% 4 Μίτσελ 78% 91%

Σχετικές στατιστικές δοκιμές

Εναλλακτικές λύσεις στο t-test για προβλήματα θέσης

Το t-test παρέχει έναν ακριβή έλεγχο για την ισότητα των μέσων όρων δύο i.i.d. κανονικών πληθυσμών με άγνωστες, αλλά ίσες, διακυμάνσεις. (Το t-test του Welch είναι ένα σχεδόν ακριβές τεστ για την περίπτωση όπου τα δεδομένα είναι κανονικά αλλά οι αποκλίσεις μπορεί να διαφέρουν). Για μέτρια μεγάλα δείγματα και ένα μονόπλευρο τεστ, το t-test είναι σχετικά ανθεκτικό σε μέτριες παραβιάσεις της παραδοχής της κανονικότητας. Σε αρκετά μεγάλα δείγματα, το t-test προσεγγίζει ασυμπτωτικά το z-test και γίνεται ανθεκτικό ακόμη και σε μεγάλες αποκλίσεις από την κανονικότητα.

Εάν τα δεδομένα είναι ουσιαστικά μη κανονικά και το μέγεθος του δείγματος είναι μικρό, το t-test μπορεί να δώσει παραπλανητικά αποτελέσματα. Βλέπε Δοκιμή θέσης για κατανομές μείγματος κλίμακας Γκαουσιανής για κάποια θεωρία που σχετίζεται με μια συγκεκριμένη οικογένεια μη κανονικών κατανομών.

Όταν η υπόθεση της κανονικότητας δεν ισχύει, μια μη παραμετρική εναλλακτική λύση του t-test μπορεί να έχει καλύτερη στατιστική ισχύ. Ωστόσο, όταν τα δεδομένα δεν είναι κανονικά με διαφορετικές αποκλίσεις μεταξύ των ομάδων, το t-test μπορεί να έχει καλύτερο έλεγχο σφάλματος τύπου 1 από ορισμένες μη παραμετρικές εναλλακτικές λύσεις.Επιπλέον, οι μη παραμετρικές μέθοδοι, όπως το τεστ Mann-Whitney U που αναλύεται παρακάτω, συνήθως δεν ελέγχουν για διαφορά μέσων όρων, οπότε θα πρέπει να χρησιμοποιούνται προσεκτικά εάν η διαφορά μέσων όρων είναι πρωταρχικού επιστημονικού ενδιαφέροντος. Επίσης, θα διαθέτει ισχύ στην ανίχνευση μιας εναλλακτικής λύσης κατά την οποία η ομάδα Β έχει την ίδια κατανομή με την Α, αλλά μετά από κάποια μετατόπιση κατά μια σταθερά (στην περίπτωση αυτή θα υπήρχε πράγματι διαφορά στους μέσους των δύο ομάδων). Εν τούτοις, θα μπορούσαν να υπάρξουν περιπτώσεις όπου η ομάδα Α και Β θα έχουν διαφορετικές κατανομές αλλά με τους ίδιους μέσους όρους (όπως δύο κατανομές, η μία με θετική λοξότητα και η άλλη με αρνητική, αλλά μετατοπισμένες έτσι ώστε να έχουν τους ίδιους μέσους όρους). Σε τέτοιες περιπτώσεις, η MW θα μπορούσε να έχει ισχύ μεγαλύτερη από το επίπεδο άλφα στην απόρριψη της μηδενικής υπόθεσης, αλλά η απόδοση της ερμηνείας της διαφοράς των μέσων όρων σε ένα τέτοιο αποτέλεσμα θα ήταν λανθασμένη.

Με την παρουσία ενός ακραίου στοιχείου, το t-test δεν είναι αξιόπιστο. Επί παραδείγματι, για δύο ανεξάρτητα δείγματα, όταν οι κατανομές των δεδομένων είναι ασύμμετρες (δηλαδή οι κατανομές είναι λοξές) ή οι κατανομές έχουν μεγάλες ουρές, τότε το τεστ Wilcoxon rank-sum test (επίσης γνωστό ως τεστ Mann-Whitney U) μπορεί να έχει τρεις έως τέσσερις φορές μεγαλύτερη ισχύ από το t-test. Το μη παραμετρικό αντίστοιχο του t-test για ζεύγη δείγματα είναι το Wilcoxon signed-rank test για ζεύγη δείγματα. Για μια συζήτηση σχετικά με την επιλογή μεταξύ του t-test και των μη παραμετρικών εναλλακτικών, βλέπε Lumley, et al. (2002).

Η μονόδρομη ανάλυση διακύμανσης (ANOVA) γενικεύει το t-test δύο δειγμάτων όταν τα δεδομένα ανήκουν σε περισσότερες από δύο ομάδες.

Ένας σχεδιασμός που περιλαμβάνει ζεύγη παρατηρήσεων και ανεξάρτητες παρατηρήσεις

Όταν υπάρχουν τόσο ζεύγη παρατηρήσεων όσο και ανεξάρτητες παρατηρήσεις στον σχεδιασμό δύο δειγμάτων, υποθέτοντας ότι τα δεδομένα λείπουν εντελώς τυχαία (MCAR), οι παρατηρήσεις με ζεύγη ή οι ανεξάρτητες παρατηρήσεις μπορούν να απορριφθούν προκειμένου να προχωρήσουμε με τους παραπάνω τυπικούς ελέγχους. Εναλλακτικά κάνοντας χρήση όλων των διαθέσιμων δεδομένων, υποθέτοντας κανονικότητα και MCAR, θα μπορούσε να χρησιμοποιηθεί ο γενικευμένος έλεγχος t μερικώς επικαλυπτόμενων δειγμάτων.

Πολυμεταβλητές δοκιμές

Μια γενίκευση του στατιστικού t του Student, που ονομάζεται στατιστικό t-τετράγωνο του Χότελινγκ, επιτρέπει τον έλεγχο υποθέσεων για πολλαπλές (συχνά συσχετιζόμενες) μετρήσεις στο ίδιο δείγμα. Παραδείγματος χάριν, ένας ερευνητής μπορεί να υποβάλει έναν αριθμό υποκειμένων σε ένα τεστ προσωπικότητας που αποτελείται από πολλαπλές κλίμακες προσωπικότητας (π.χ. το Πολυφασικό Τεστ Προσωπικότητας της Μινεσότα). Επειδή οι μετρήσεις αυτού του τύπου είναι συνήθως θετικά συσχετισμένες, δεν είναι σκόπιμο να διεξάγονται ξεχωριστές μονομεταβλητές δοκιμές t για τον έλεγχο των υποθέσεων, καθώς αυτές θα παραμελούσαν τη συνδιακύμανση μεταξύ των μετρήσεων και θα διόγκωναν την πιθανότητα λανθασμένης απόρριψης τουλάχιστον μιας υπόθεσης (σφάλμα τύπου Ι). Σε αυτή την περίπτωση είναι προτιμότερο να διενεργείται ένας ενιαίος πολυμεταβλητός έλεγχος για τον έλεγχο υποθέσεων. Η μέθοδος του Φίσερ για το συνδυασμό πολλαπλών δοκιμών με μειωμένο άλφα για θετική συσχέτιση μεταξύ των δοκιμών είναι μία. Μια άλλη είναι η στατιστική T² του Χότελινγκ που ακολουθεί την κατανομή T² . Ωστόσο, στην πράξη η κατανομή αυτή χρησιμοποιείται σπάνια, δεδομένου ότι είναι δύσκολο να βρεθούν ταξινομημένες τιμές για το T² . Συνήθως, το T² μετατρέπεται αντί αυτού σε στατιστική F.

Για έναν πολυμεταβλητό έλεγχο ενός δείγματος, η υπόθεση είναι ότι το μέσο διάνυσμα (Πρότυπο:Math) είναι ίσο με ένα δεδομένο διάνυσμα (Πρότυπο:Math). Το στατιστικό του ελέγχου είναι το t²: του Χότελινγκ:

$t^2=n(\overline{𝐱}-{\mathit{\mu }}_0{)}^{\prime }{𝐒}^{-1}(\overline{𝐱}-{\mathit{\mu }}_0)$

όπου Πρότυπο:Math είναι το μέγεθος του δείγματος, Πρότυπο:Math είναι το διάνυσμα των μέσων όρων στήλης και Πρότυπο:Math είναι ένας Πρότυπο:Math πίνακας συνδιακύμανσης δείγματος.

Για έναν πολυμεταβλητό έλεγχο δύο δειγμάτων, η υπόθεση είναι ότι τα μέσα διανύσματα (Πρότυπο:Math) δύο δειγμάτων είναι ίσα. Το στατιστικό του ελέγχου είναι το T² δύο δειγμάτων του Χότελινγκ:

$t^2=\frac{n_1{n}_2}{n_1+n_2}({\overline{𝐱}}_1-{\overline{𝐱}}_2){{𝐒}_{\text{pooled}}}^{-1}({\overline{𝐱}}_1-{\overline{𝐱}}_2).$

Το t-test δύο δειγμάτων αποτελεί ειδική περίπτωση της απλής γραμμικής παλινδρόμησης

Το t-test δύο δειγμάτων αποτελεί ειδική περίπτωση της απλής γραμμικής παλινδρόμησης, όπως φαίνεται στο ακόλουθο παράδειγμα.

Μια κλινική δοκιμή εξετάζει 6 ασθενείς στους οποίους χορηγείται φάρμακο ή εικονικό φάρμακο. Τρεις (3) ασθενείς λαμβάνουν 0 μονάδες φαρμάκου (η ομάδα εικονικού φαρμάκου). Τρεις (3) ασθενείς λαμβάνουν 1 μονάδα φαρμάκου (η ομάδα ενεργού θεραπείας). Στο τέλος της θεραπείας, οι ερευνητές μετρούν τη μεταβολή από την αρχική τιμή στον αριθμό των λέξεων που μπορεί να ανακαλέσει κάθε ασθενής σε ένα τεστ μνήμης.

Παρακάτω παρουσιάζεται ένας πίνακας με την ανάκληση των λέξεων και τις τιμές της δόσης του φαρμάκου των ασθενών.

Ασθενής	φαρμακευτική δόση	λέξη.ανάκληση
1	0	1
2	0	2
3	0	3
4	1	5
5	1	6
6	1	7

Ο πίνακας των συντελεστών δίνει τα ακόλουθα αποτελέσματα.

• Η εκτιμώμενη τιμή 2 για την τομή είναι η μέση τιμή της ανάκλησης λέξης όταν η δόση του φαρμάκου είναι 0.
• Η τιμή εκτίμησης 4 για τη δόση φαρμάκου δείχνει ότι για μια μεταβολή της δόσης φαρμάκου κατά 1 μονάδα (από 0 σε 1) υπάρχει μεταβολή 4 μονάδων στη μέση ανάκληση λέξεων (από 2 σε 6). Αυτή είναι η κλίση της ευθείας που ενώνει τους μέσους όρους των δύο ομάδων.
• Το p-τιμή ότι η κλίση 4 είναι διαφορετική από το 0 είναι p = 0,00805.

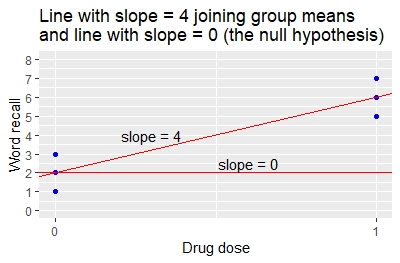
Οι συντελεστές της γραμμικής παλινδρόμησης καθορίζουν την κλίση και την τομή της ευθείας που ενώνει τους μέσους όρους των δύο ομάδων, όπως απεικονίζεται στο γράφημα. Η τομή είναι 2 και η κλίση είναι 4.

Σύγκριση του αποτελέσματος από τη γραμμική παλινδρόμηση με το αποτέλεσμα από το t-test.

• Από το t-test, η διαφορά μεταξύ των μέσων όρων των ομάδων είναι 6-2=4.
• Από την παλινδρόμηση, η κλίση είναι επίσης 4, υποδεικνύοντας ότι μια αλλαγή 1 μονάδας στη δόση του φαρμάκου (από 0 σε 1) δίνει μια αλλαγή 4 μονάδων στη μέση ανάκληση λέξεων (από 2 σε 6).
• Το t-test p-τιμή για τη διαφορά στους μέσους όρους, και η p-τιμή της παλινδρόμησης για την κλίση, είναι και οι δύο 0,00805. Οι μέθοδοι δίνουν πανομοιότυπα αποτελέσματα.

Αυτό το παράδειγμα δείχνει ότι, για την ειδική περίπτωση της απλής γραμμικής παλινδρόμησης όπου υπάρχει μία μόνο μεταβλητή x που έχει τιμές 0 και 1, ο t-test δίνει τα ίδια αποτελέσματα με τη γραμμική παλινδρόμηση. Η σχέση μπορεί επίσης να παρουσιαστεί αλγεβρικά.

Η αναγνώριση αυτής της σχέσης μεταξύ του t-test και της γραμμικής παλινδρόμησης διευκολύνει τη χρήση της πολλαπλής γραμμικής παλινδρόμησης και της πολυδιάστατης ανάλυσης διακύμανσης. Αυτές οι εναλλακτικές λύσεις των t-tests επιτρέπουν τη συμπερίληψη πρόσθετων επεξηγηματικών μεταβλητών που σχετίζονται με την απόκριση. Η συμπερίληψη τέτοιων πρόσθετων επεξηγηματικών μεταβλητών με τη χρήση παλινδρόμησης ή anova μειώνει την κατά τα άλλα ανεξήγητη διακύμανση και συνήθως αποδίδει μεγαλύτερη ισχύ για την ανίχνευση διαφορών από ό,τι οι t-test δύο δειγμάτων.

Εφαρμογές λογισμικού

Πολλά προγράμματα λογιστικά φύλλα και στατιστικά πακέτα, όπως QtiPlot, LibreOffice Calc, Microsoft Excel, SAS, SPSS, Stata, DAP, gretl, R, Python, PSPP, Wolfram Mathematica, MATLAB και Minitab, περιλαμβάνουν υλοποιήσεις του t-test του Student.

Γλώσσα/Πρόγραμμα	Λειτουργία	Σημειώσεις
Microsoft Excel pre 2010	TTEST(array1, array2, tails, type)	Βλ. [1]
Microsoft Excel 2010 and later	T.TEST(array1, array2, tails, type)	Βλ.[2]
Apple Numbers	TTEST(sample-1-values, sample-2-values, tails, test-type)	Βλ.[3]
LibreOffice Calc	TTEST(Data1; Data2; Mode; Type)	Βλ. [4]
Google Sheets	TTEST(range1, range2, tails, type)	Βλ. [5]
Python	scipy.stats.ttest_ind(a, b, equal_var=True)	Βλ. [6]
MATLAB	ttest(data1, data2)	Βλ. [7]
Mathematica	TTest[{data1,data2}]	Βλ. [8]
R	t.test(data1, data2, var.equal=TRUE)	Βλ. [9]
SAS	PROC TTEST	Βλ. [10]
Java	tTest(sample1, sample2)	Βλ. [11]
Julia	EqualVarianceTTest(sample1, sample2)	Βλ. [12]
Stata	ttest data1 == data2	Βλ. [13]

Εξωτερικοί σύνδεσμοι

• English - Greek Dictionary of Pure and Applied Mathematics Εθνικό Μετσόβιο Πολυτεχνείο
• Αγγλοελληνικό Λεξικό Μαθηματικής Ορολογίας - Πανεπιστήμιο Κύπρου
• Ευκλείδεια Γεωμετρία - Πανελλήνιο Σχολικό Δίκτυο
• Θεωρία ομάδων και Λι αλγεβρών -Εθνικό Αρχείο Διδακτορικών Διατριβών
• Θεωρία Αριθμών και Εφαρμογές
• Υπολογιστική Θεωρία Αριθμών
• Καμπυλότητες και γεωμετρία του Riemann σε διαφορίσιμες πολλαπλότητες Εθνικό Αρχείο Διδακτορικών Διατριβών
• Μέθοδοι μηχανικής μάθησης βασισμένες σε έλεγχο μονοτροπικότητας Εθνικό Αρχείο Διδακτορικών Διατριβών
• Παράμετροι και Στατιστικά. Διωνυμική και Κανονική Κατανομή

Δείτε επίσης

• Απαγορευτική αρχή του Πάουλι
• Κατανομή t-Student
• Κανονική κατανομή
• Αλγεβρική θεωρία αριθμών
• Διαφορική γεωμετρία
• Άρθουρ Στάνλεϋ Έντινγκτον
• Θεωρία αναπαραστάσεων
• Σουμπραμανιάν Τσαντρασεκάρ
• Ευκλείδειος χώρος
• Ένα προς ένα
• Σουμπραμανιάν Τσαντρασεκάρ
• Εφαρμοσμένα μαθηματικά
• Προβολικός χώρος
• Διακριτός μετασχηματισμός Φουριέ
• Θεμελιώδες θεώρημα αριθμητικής
• Αλγεβρική γεωμετρία
• Μιγαδικός αριθμός
• Άρθουρ Στάνλεϋ Έντινγκτον
• Τυπική απόκλιση

Βιβλιογραφία

• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book

Παραπομπές

• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite journal [14] (15 pages)
• Πρότυπο:Cite journal
• Πρότυπο:Cite book
• Πρότυπο:Cite journal
• Πρότυπο:Cite journal
• Πρότυπο:Cite book Ch. 1–6 of 2013 edition

Πηγές

• Πρότυπο:Citation
• Πρότυπο:Citation
• Πρότυπο:Citation
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Citation
• Πρότυπο:Citation