Αρχείο:Heatequation exampleB.gif
Αυτό το αρχείο είναι από το Wikimedia Commons και ενδέχεται να χρησιμοποιείται από άλλα εγχειρήματα. Η περιγραφή στη σελίδα περιγραφής του εκεί, εμφανίζεται παρακάτω.
Σύνοψη
| ΠεριγραφήHeatequation exampleB.gif |
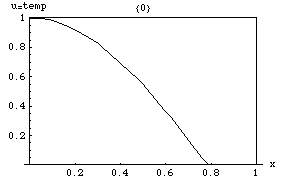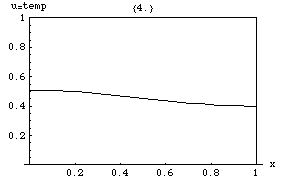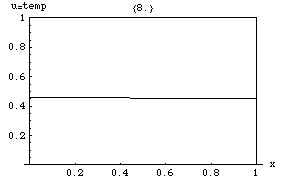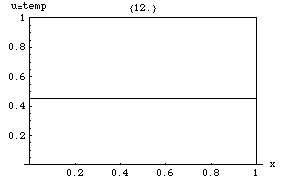
English: General audience description: Here the horizontal axis represents the location along a bar of metal and the graph records the temperature at that location. It begins with an initial temperature which is hot at one side and cool at the other, and then shows how the temperature of the bar approaches an equilibrium. It is assumed that no heat is lost from the bar and that there are no heat sources. This demonstrates two key properties of the heat equation: approaching an equilibrium, and the maximum principle. The maximum principle says that the temperature will always have a maximum either earlier in time or at the ends of the bar. Description: where k = .061644 subject to the boundary conditions: and with the initial heat distribution given by: In this case, the left face (x=0) and the right face (x=1) are perfectly insulated. This image shows how the heat redistributes, flowing from the warmer left edge to the cooler right edge, then equalizing to a constant temperature throughout. This temperature happens to be the average value of cos(2x) over [0,1], as one might expect. The solution: where: Solution details: |
||
| Πηγή | Έργο αυτού που το ανεβάζει | ||
| Δημιουργός | User:Wtt | ||
| άλλες εκδόσεις |
|
||
| Source code InfoField | Mathematica Source:
j = 10;
k = .061644;
A[n_] := (-4 (-1)^n* Sin[2])/(-4 + n^2*Pi^2);
u[x_, t_] := Sin[2]/2 + Sum[A[n]*Cos[n*Pi*x]*Exp[-k(n*Pi)^2*t], {n, 1, j}];
For[i = 0, i <= 12, i += .1,
Print@Plot[u[x, i], {x, 0, 1},
Prolog -> {Line[{{0, 1}, {1, 1}, {1, 1}, {1, 0}}]},
PlotRange -> {0, 1},
AxesLabel -> {"x", "u=temp"},
PlotLabel -> {i}
]
]
|
Αδειοδότηση

|
Παραχωρείται η άδεια προς αντιγραφή, διανομή και/ή τροποποίηση αυτού του εγγράφου υπό τους όρους της Άδειας Ελεύθερης Τεκμηρίωσης GNU, Έκδοση 1.2 ή οποιασδήποτε νεότερης έκδοσης δημοσιευμένης από το Ίδρυμα Ελεύθερου Λογισμικού· χωρίς Απαράλαχτους Τομείς, χωρίς Κείμενα Εξωφύλλου, και χωρίς Κείμενα Οπισθοφύλλου. Αντίγραφο της άδειας περιλαμβάνεται στην σελίδα με τίτλο GNU Free Documentation License.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
| Το αρχείο διανέμεται υπό την άδεια Creative Commons Αναφορά προέλευσης-Παρόμοια διανομή 3.0 Μη εισαγόμενη | ||
| ||
| Αυτή η ετικέτα άδειας χρήσης προστέθηκε στο αρχείο ως μέρους της αναθεώρησης της άδειας GFDL .http://creativecommons.org/licenses/by-sa/3.0/CC BY-SA 3.0Creative Commons Attribution-Share Alike 3.0truetrue |
- Είστε ελεύθερος:
- να μοιραστείτε – να αντιγράψετε, διανέμετε και να μεταδώσετε το έργο
- να διασκευάσετε – να τροποποιήσετε το έργο
- Υπό τις ακόλουθες προϋποθέσεις:
- αναφορά προέλευσης – Θα πρέπει να κάνετε κατάλληλη αναφορά, να παρέχετε σύνδεσμο για την άδεια και να επισημάνετε εάν έγιναν αλλαγές. Μπορείτε να το κάνετε με οποιοδήποτε αιτιολογήσιμο λόγο, χωρίς όμως να εννοείται με οποιονδήποτε τρόπο ότι εγκρίνουν εσάς ή τη χρήση του έργου από εσάς.
- παρόμοια διανομή – Εάν αλλάξετε, τροποποιήσετε ή δημιουργήσετε πάνω στο έργο αυτό, μπορείτε να διανείμετε αυτό που θα προκύψει μόνο υπό τους όρους της ίδιας ή συμβατής άδειας με το πρωτότυπο.
Λεζάντες
Τα Αντικείμενα που απεικονίζονται σε αυτό το αρχείο
απεικονίζει
Ιστορικό αρχείου
Πατήστε σε μια ημερομηνία/ώρα για να δείτε το αρχείο όπως εμφανιζόταν εκείνη την χρονική στιγμή.
| Ημερομηνία/Ώρα | Μικρογραφία | Διαστάσεις | Χρήστης | Σχόλιο | |
|---|---|---|---|---|---|
| τρέχον | 23:01, 17 Απριλίου 2007 |  | 288 × 177 (30 KB) | wikimediacommons>Wtt~commonswiki |
Χρήση αρχείου
Η ακόλουθη σελίδα χρησιμοποιεί προς αυτό το αρχείο: