Υπεργράφημα

Πρότυπο:Υπό μετάφρασηΣτα μαθηματικά, υπεργράφημα είναι μια γενίκευση της έννοιας του γραφήματος, στην οποία μια ακμή μπορεί να συνδέσει οσοδήποτε μεγάλο πλήθος κορυφών. Σε αντιδιαστολή, στα συνήθη γραφήματα κάθε ακμή συνδέει ακριβώς δύο κορυφές (όχι κατ' ανάγκη διακεκριμένες).

Ένα παράδειγμα ενός μη κατευθυνόμενου υπεργραφήματος, με $X=\{v_1,v_2,v_3,v_4,v_5,v_6,v_7\}$ και $E=\{e_1,e_2,e_3,e_4\}=\{\{v_1,v_2,v_3\},\{v_2,v_3\},$ $\{v_3,v_5,v_6\},\{v_4\}\}$ Αυτό το υπεργράφημα έχει τάξη επτά και μέγεθος τέσσερα. Παρατηρήστε ότι οι έδρες (οι οποίες αναπαρίστανται με χρωματιστές περιοχές) δεν συνδέουν απλώς δύο κορυφές, αλλά περισσότερες.

Τυπικά, ένα μη κατευθυνόμενο υπεργράφημα $H$ είναι ένα διατεταγμένο ζεύγος $H=(X,E)$, όπου $X$ είναι ένα σύνολο του οποίου τα στοιχεία ονομάζονται κορυφές, και το $E$ είναι ένα σύνολο μη κενών υποσυνόλων του $X$, δηλαδή $E\in 𝒫(X)\mathrm{\setminus }\{\mathrm{\varnothing }\}$. Τα στοιχεία του $E$ καλούνται ακμές ή υπερακμές, οπότε γι' αυτό καμιά φορά τα $X$ και $E$ καλούνται σύνολο κορυφών και σύνολο ακμών (ή υπερακμών) αντίστοιχα. Ο πληθάριθμος του συνόλου κορυφών $X$ καλείται τάξη του υπεργραφήματος και ο πληθάριθμος του συνόλου ακμών $E$ καλείται μέγεθος του υπεργραφήματος.

Τα κατευθυνόμενα υπεργραφήματα διαφέρουν από τα μη κατευθυνόμενα υπεργραφήματα στις ακμές - οι υπερακμές δεν είναι πλέον σύνολα, αλλά διατεταγμένα ζεύγη στοιχείων του $X$.

Όπως ήδη αναφέρθηκε, οι ακμές των συνήθων γραφημάτων συνδέουν μόνο δύο κορυφές, ενώ οι υπερακμές δεν έχουν κάποιο περιορισμό ως προς το πλήθος των κορυφών που συνδέουν. Παρ' όλα αυτά, συνήθως είναι επιθυμητό να μελετηθούν υπεργραφήματα στα οποία όλες οι υπερακμές συνδέουν το ίδιο πλήθος κορυφών, δηλαδή οι πληθάριθμοι των υπερακμών ισούνται. Τέτοιου είδους γραφήματα όπου για κάθε $e\in E$ αληθεύει $|e|=k$, ονομάζονται $k-$ομοιόμορφα υπεργραφήματα. Μ' αυτόν τον ορισμό, ένα $2-$ομοιόμορφο υπεργράφημα είναι ένα σύνηθες γράφημα, ένα $3-$ομοιόμορφο υπεργράφημα είναι ένα υπεργράφημα του οποίου οι ακμές συνδέουν τρεις κορυφές κ.ο.κ. Ένα μη κατευθυνόμενο υπεργράφημα καλείται επίσης σύστημα συνόλων ή οικογένεια συνόλων επιλεγόμενη από τον κόσμο αντικειμένων (ο κόσμος με την συνολοθεωρητική έννοια).

Τα υπεργραφήματα μπορούν να ειδωθούν ως δομές πρόσπτωσης. Συγκεκριμένα, υπάρχει ένα διμερές "γράφημα προσπτώσεων" ή αλλιώς "γράφημα Levi" που αντιστοιχεί σε κάθε υπεργράφημα. Κατ' επέκταση, πολλά (αλλά όχι όλα) τα διμερή γραφήματα μπορούν να ειδωθούν ως γραφήματα προσπτώσεων υπεργραφημάτων.

Τα υπεργραφήματα εμφανίζονται συχνά στον χώρο των μαθηματικών, με διάφορες ονομασίες. Στην υπολογιστική γεωμετρία, τα μη κατευθυνόμενα γραφήματα καλούνται range spaces και οι υπερακμές ranges. Στην συνεργατική θεωρία παιγνίων, τα υπεργραφήματα ονομάζονται απλά παιχνίδια (παιχνίδια ψήφων) - αυτή η ιδέα χρησιμοποιείται για την επίλυση προβλημάτων στη θεωρία της κοινωνικής επιλογής (social choice theory). Μερικές φορές στη βιβλιογραφία οι ακμές ονομάζονται υπεσύνδεσμοι ή σύνδεσμοι.

Η οικογένεια των υπεργραφημάτων είναι μια κατηγορία με μορφισμούς τους ομομορφισμούς των υπεργραφημάτων.

Μία εναλλακτική αναπαράσταση του υπεργραφήματος της προηγούμενης εικόνας, η οποία ονομάζεται αναπαράσταση PAOH. Οι ακμές είναι οι κατακόρυφες γραμμές που εννώνουν τις κορυφές. Η κορυφή $v_7$ είναι, αυτό που λέμε, μεμονωμένη κορυφή. Ο πίνακας στα δεξιά δίνει τα ονόματα των ακμών.

Ένα παράδειγμα ενός κατευθυνόμενου υπεργραφήματος με $X=\{1,2,3,4,5,6\}$ και $E=\{(\{1\},\{2\}),(\{2\},\{3\}),(\{3\},\{1\}),$$(\{2,3\},\{4,5\}),(\{3,5\},\{6\})\}$

Εφαρμογές

Τα μη κατευθυνόμενα υπεργραφήματα είναι χρήσιμα στη μοντελοποίηση προβλημάτων satisfiability, στις βάσεις δεδομένων, στην εκμάθηση μηχανών και στα προβλήματα δένδρων, του Steiner. Ιδίως στην εκμάθηση μηχανών, τα υπεργραφήματα έχουν χρησιμοποιηθεί ευραίως στην μοντελοποίηση δεδομένων και στην κανονικοποίηση (regularization). Οι εφαρμογές τους επίσης περιλαμβάνουν τα recommender systems (οι κοινότητες αναπαρίστανται ως υπερακμές), στο image retrieval (οι εξαρτήσεις αναπαρίστανται ως υπερακμές), και στα bioinformatics (οι βιοχημικές αλληλεπιδράσεις αναπαρίστανται ως υπερακμές). Αντιπροσωπευτικές τεχνικές εκμάθησης με υπεργραφήματα περιλαμβάνουν το spectral clustering των υπεργραφημάτων (το οποίο επεκτείνει την spectral γραφοθεωρία με Laplacianές υπεργραφημάτων) και το semi-supervised learning των υπεργραφημάτων (το οποίο εισάγει επιπλέον κόστος στη δομή του υπεργραφήματος, για να περιορίσει τα αποτελέσματα της εκμάθησης). Για μεγάλα υπεργραφήματα, είναι διαθέσιμο ένα distributed framework build, το οποίο χρησιμοποιεί το Apache Spark.

Τα κατευθυνόμενα υπεργραφήματα μπορούν να χρησιμοποιηθούν στην μοντελοποίηση, για παράδειγμα στην τηλεφωνία, στην ανίχνευση ξεπλήματος χρήματος, στο operation research, και στον προγραμματισμό των μεταφορών. Είναι επίσης δυνατόν να μοντελοποιήσουν την Horn-satisfiability.

Γενικεύσεις εννοιών από τα συνήθη γραφήματα

Πολλά θεωρήματα και έννοιες των απλών γραφημάτων μεταβιβάζονται σχεδόν αυτούσια στα υπεργραφήματα. Συγκεκριμένα, στα μη κατευθυνόμενα υπεργραφήματα:

• Το ταίριασμα στα υπεργραφήματα,
• Τα καλύμματα κορυφών στα υπεργραφήματα,
• Ο γραμμογράφος (line graph) ενός υπεργραφήματος,
• Η γραμματική των υπεργραφημάτων,
• Το θεώρημα του Ramsey,
• Το θεώρημα Erdős–Ko–Rado,
• Το θεώρημα Kruskai-Katona, στα ομοιόμορφα υπεργραφήματα,
• Θεωρήματα τύπου Hall για υπεργραφήματα.

Στα κατευθυνόμενα υπεργραφήματα: η μεταβατική κλειστότητα, και τα προβλήματα εύρεσης συντομότερου μονοπατιού.

Αναπαραστάσεις υπεργραφημάτων

Παρά τη δυσκολία αναπαράστασης των υπεργραφημάτων (τουλάχιστον δυσκολότερη από την αναπαράσταση των συνήθων γραφημάτων), έχει υπάρξει από αρκετούς ερευνητές μελέτη όσον αφορά την οπτικοποίηση των υπεργραφημάτων.

Ένας τρόπος αναπαράστασης των υπεργραφημάτων είναι παρόμοιος με αυτόν της αναπαράστασης των συνήθων γραφημάτων - οι κορυφές του υπεργραφήματος σχεδιάζονται ως σημεία, ορθογώνια, δίσκοι κ.ο.κ. στο επίπεδο, ενώ οι υπερακμές ως δέντρα που έχουν τις κορυφές ως φύλλα τους. Εάν συγκεκριμμένα οι κορυφές αναπαρίστανται ως σημεία, οι υπερακμές ενδέχεται να αναπαρίστανται ως λείες καμπύλες που εννώνουν τα σημεία, ή απλές κλειστές καμπύλες που τα περικλύουν.

Υπάρχουν κι άλλοι τρόποι αναπαράστασης υπεργραφημάτων, κι ένας εκ των οποίων είναι η αναπαράσταση μέσω υποδιαίρεσης. Το επίπεδο χωρίζεται σε περιοχές, καθεμία εκ των οποίων αντιπροσωπεύει μια κορυφή του υπεργραφήματος. Οι υπερακμές αναπαρίστανται ως ένωση υποσυνόλων των περιοχών που χρωματίζονται ή σχεδιάζονται τα περιγράμματά τους (ή και τα δύο). Ένα τάξεως$-n$ διάγραμμα Venn, για παράδειγμα, μπορεί να ειδωθεί ως μια αναπαράσταση με υποδιαίρεση ενός υπεργραφήματος με $n$ υπερακμές (οι καμπύλες ορίζουν το διάγραμμα) και $2^n-1$ κορυφές (οι οποίες αναπαρίστανται από περιοχές και είναι αποτέλεσμα της τομής του επιπέδου από τις προαναφερόμενες καμπύλες). Σε αντίθεση με τον πολυωνυμικό χρόνο που χρειάζεται για να εξακριβωθεί (υπολογιστικά) εάν ένα γράφημα είναι επιπεδικό, είναι NP-πλήρες πρόβλημα να εξακριβωθεί εάν ένα υπεργράφημα έχει επιπεδική αναπαράσταση μέσω υποδιαίρεσης - παρόλα αυτά, η ύπαρξη μιας αναπαράστασης τέτοιου τύπου μπορεί να ελεγχθεί αποτελεσματικά όταν οι περιοχές εφάπτονται με τέτοιον τρόπο ώστε να σχηματίζουν μονοπάτι, κύκλο ή δέντρο.

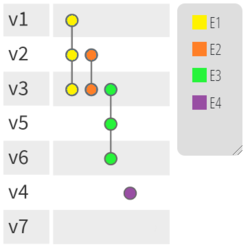
Ένας εναλλακτικός τρόπος αναπαράστασης είναι ο PAOH, ο οποίος εικονίζεται στο δεύτερο σχήμα. Οι ακμές σχεδιάζονται ως κατακόρυφες γραμμές που εννώνουν κορυφές. Οι κορυφές βρίσκονται στα αριστερά. Η λεζάντα στα δεξιά δείχνει τα ονόματα των ακμών. Συγκεκριμένα αυτός ο τρόπος αναπαράστασης υπεργραφημάτων έχει σχεδιαστεί για δυναμικά υπεργραφήματα, αλλά μπορεί να χρησιμοποιηθεί γενικά σε υπεργραφήματα.

Αυτό το κύκλωμα μπορεί να ειδωθεί ως αναπαράσταση υπεργραφήματος με τέσσερεις κορυφές (οι οποίες είναι τα ορθογώνια και οι δίσκοι) και με τρεις υπερακμές (οι οποίες είναι σχεδιασμένες ως δέντρα με φύλλα τις κορυφές).

Ένα τάξης$-4$ διάγραμμα Venn, το οποίο μπορεί να αναπαραστεθεί μέσω υποδιαίρεσης ως υπεργράφημα με δεκαπέντε κορυφές (οι δεκαπέντε χρωματιστές περιοχές) και με τέσσερεις υπερακμές (τα τέσσερα ελλείπτικά χωρία).

Κάθε πεπερασμένο προβολικό επίπεδο

$n^2+n+1$

σημείων μπορεί να ειδωθεί ως αναπαράσταση ενός

$(n+1)-$

ομοιόμορφου υπεργραφήματος με

$n^2+n+1$

κορυφές. Να σημειωθεί ότι το πλήθος των κορυφών δεν είναι περιοριστικό, αφού κάθε προβολικό επίπεδο έχει

$n^2+n+1$

σημεία, για κάποιον

$n$

.

Το προβολικό επίπεδο του Fano μπορεί να ειδωθεί ως αναπαράσταση ενός υπεργραφήματος με επτά κορυφές και επτά ακμές. Οι κορυφές του αναπαρίστανται ως σημεία και οι ακμές του ως γραμμές (ευθύγραμμα τμήματα ή κύκλοι) που περιέχουν τρεις κορυφές.

Χρωματισμοί υπεργραφημάτων

Ο κλασικός χρωματισμός υπεργραφημάτων είναι μια αντιστοιχία $𝔵:X\to [\lambda ]$ αριθμών στο $[\lambda ]=\{1,2,3,\cdots ,\lambda \}$ (οι οποίοι ονομάζονται χρώματα) από κάθε κορυφή του υπεργραφήματος, με τρόπο τέτοιο ώστε κάθε υπερακμή να περιέχει κατ' ελάχιστο δύο κορυφές διαφορετικού χρώματος. Με άλλα λόγια, δεν θα πρέπει να υπάρχει μονοχρωματική υπερακμή με πληθικότητα τουλάχιστον $2$ (για κάθε ακμή $e\in E$, αληθεύει $|𝔵(e)|⩾2$). Κατά κάποιον τρόπο, είναι μια γενίκευση του χρωματισμού των συνήθων γραφημάτων. Ο ελάχιστος αριθμός χρωμάτων που χρειάζονται ώστε ώστε να επιτευχθεί ένας χρωματισμός καλείται χρωματικός αριθμός του υπεργραφήματος.

Τα υπεργραφήματα για τα οποία υπάρχει χρωματισμός που χρησιμοποιεί το πολύ $k-$χρώματα ονομάζονται $k-$χρωματίσιμα. Τα $2-$χρωματίσιμα υπεργραφήματα είναι ακριβώς τα διμερή.

Υπάρχουν πολλές γενικεύσεις του κλασικού χρωματισμού των υπεργραφημάτων. Ένας εξ' αυτών ονομάζεται χρωματισμός των αναμεμειγμένων υπεργραφημάτων (mixed hypergraph coloring).

Ένα αναμεμειγμένο υπεργράφημα $H$ με σύνολο κορυφών $X$ είναι μία διατεταγμένη τριάδα $(X,C,D)$ τέτοια ώστε τα $C$ και $D$ να είναι οικογένειες υποσυνόλων του $X$ (δηλαδή $C,D\in 𝒫(X)$). Τα στοιχεία των $C$ και $D$ ονομάζονται $C-$ακμές και $D-$ακμές αντίστοιχα. Ένας χρωματισμός $𝔵:X\to [\lambda ]$ του αναμεμειγμένου υπεργραφήματος $H$ με $\lambda$ χρώματα είναι μια αντιστοιχία σε αριθμούς του $[\lambda ]$ από κορυφές του υπεργραφήματος, έτσι ώστε κάθε $C$ και $D-$ακμή να περιέχει κατ' ελάχιστο δύο κορυφές διαφορετικού χρώματος (δηλαδή $\mathrm{\forall }e\in C\cup D,|𝔵(e)|⩾2$). Το ελάχιστο πλήθος χρωμάτων που χρειάζεται για να επιτευχθεί ένας τέτοιος χρωματισμός καλείται χρωματικός αριθμός του υπεργραφήματος και συμβολίζεται με $\chi (H)$. Αντίστοιχα, το μέγιστο πλήθος ονομάζεται άνω χρωματικός αριθμός και συμβολίζεται με $\bar{\chi }(H)$.

Να σημειωθεί ότι ένα γενικό κριτήριο μη χρωματισιμότητας δεν είναι γνωστό. Παρ' όλα αυτά, μερικές περιπτώσεις μη χρωματισιμότητας γραφημάτων ειδικού τύπου, είναι γνωστές.

• Το πλήρες $(l,m)-$ομοιόμορφο υπεργράφημα $K(n,l,m)$ (εδώ η γενίκευση του ομοιόμορφου γίνεται με τον αναμενόμενο τρόπο) είναι μη χρωματίσιμο αν και μόνο αν $n>(l-1)\cdot (m-1)$.
• Δοθέντος ενός γραφήματος $G$, ορίζουμε $H$ το αναμεμειγμένο υπεργράφημα με σύνολο κορυφών $X$ έτσι ώστε η οικογένεια $D$ να είναι οι ακμές του $G$ και η οικογένεια $C$ να είναι το σύνολο όλων των μονοπατιών μήκους $k$ στο $G$. To $H$ είναι χρωματίσιμο αν και μόνο αν $\chi (G)<k$.
• Ένα υπερδέντρο είναι ένα υπεργράφημα του οποίου οι ακμές είναι υποδέντρα ενός δοθέντος δέντρου. Ένα αναμεμειγμένο υπερδέντρο $H$ είναι χρωματίσιμο αν και μόνο αν δεν περιέχει μια φανερά μη χρωματίσιμη $D-$ακμή - δηλαδή μια ακμή στην οποία κάθε ζεύγος κορυφών περιέχεται σε μονοπάτι από $C-$ακμές μεγέθους $2$.

Ιδιότητες των υπεργραφημάτων

Ένα υπεργράφημα μπορεί να έχει διάφορες ιδιότητες. Μερικές εξ' αυτών αναγράφονται παρακάτω:

• Κενό υπεργράφημα: Ένα κενό υπεργράφημα είναι ένα υπεργράφημα χωρίς υπερακμές.
• Μη απλό: Ένα υπεργράφημα καλείται μη απλό αν έχει θηλιές ή επαναλαμβανόμενες ακμές. Δηλαδή αν έχει ακμές που ορίζονται από μοναδική κορυφή ή (διακεκριμένες) ακμές που ορίζονται από το ίδιο σύνολο κορυφών.
• Απλό: Ένα υπεργράφημα καλείται απλό αν δεν είναι μη απλό.
• $d-$κανονικό: Ένα υπεργράφημα καλείται $d-$κανονικό αν κάθε κορυφή του έχει βαθμό $d$ - δηλαδή αν κάθε κορυφή του περιέχεται ακριβώς σε $d$ ακμές.
• $2-$χρωματίσιμο: Ένα υπεργράφημα καλείται $2-$χρωματίσιμο αν υπάρχει χρωματισμός του με το πολύ δύο χρώματα. Ισοδύναμα, αν το σύνολο των κορυφών του μπορεί να διαμεριστεί σε δύο κλάσεις $U$ και $V$, έτσι ώστε κάθε υπερακμή με πληθικότητα τουλάχιστον $2$ περιέχει τουλάχιστον μία κορυφή από κάθε κλάση. Ένας εναλλακτικός όρος για το συγκεκριμένο είναι η ιδιότητα Β. Μια γενίκευση αυτού του είδους των γραφημάτων είναι τα ισορροπημένα υπεργραφήματα.
• $k-$ομοιόμορφο: Ένα υπεργράφημα καλείται $k-$ομοιόμορφο αν κάθε υπερακμή του έχει πληθικότητα ακριβώς $k$.
• $k-$μερές: Ένα υπεργράφημα ονομάζεται $k-$μερές αν το σύνολο κορυφών μπορεί να διαμεριστεί σε $k$ κλάσεις, έτσι ώστε κάθε ακμή περιέχει ακριβώς μία ακμή από κάθε κλάση. Κάθε $k-$μερές υπεργράφημα με $k⩾2$ είναι $k-$χρωματίσιμο και διμερές.
• Κάτω κλειστό: Ένα μη κατευθυνόμενο υπεργράφημα καλείται κάτω κλειστό αν κάθε υποσύνολο οποιασδήποτε ακμής είναι κι αυτό ακμή. Ένα κάτω κλειστό υπεργράφημα συνήθως ονομάζεται αφηρημένο simplicial σύμπλοκο (abstract simplicial complex).

Σχετικά υπεργραφήματα

Επειδή οι ακμές των υπεργραφημάτων μπορούν να έχουν οποιαδήποτε πληθικότητα, υπάρχουν πολλές έννοιες 'υπογραφήματος': τα υπο-υπεργραφήματα, τα μερικά υπεργραφήματα και τα τμηματικά υπεργραφήματα.

Έστω $H=(X,E)$ ένα υπεργράφημα με σύνολο κορυφών:

και σύνολο υπερακμών:

όπου $I_v,I_e$ είναι τα σύνολα δεικτών για τις κορυφές και τις ακμές αντίστοιχα.

Υπο-υπεργραφήματα και επεκτάσεις υπεργραφημάτων

Ένα υπο-υπεργράφημα είναι ένα υπεργράφημα του οποίου κάποιες κορυφές έχουν αφαιρεθεί. Τυπικά μιλώντας, ένα υπο-υπεργράφημα $H_A$ με σύνολο κορυφών $A\subseteq X$ ορίζεται ως εξής:

Ένας εναλλακτικός ορισμός είναι ο περιορισμός του $H$ στο $A$.

Επέκταση $\mathrm{E}\mathrm{x}(H_A)$ ενός υπο-υπεργραφήματος $H_A$ είναι το υπεργράφημα για το οποίο κάθε υπερακμή στο $H$ που περιέχεται μερικώς στο υπο-υπεργράφημα, περιέχεται πλήρως στην επέκταση. Αυστηρότερα:

Μερικά και δυϊκά υπεργραφήματα

Ένα μερικό υπεργράφημα είναι ένα υπεργράφημα του οποίου κάποιες ακμές έχουν αφαιρεθεί. Δοθέντος ενός υποσυνόλου $J\subset I_e$ του συνόλου δεικτών των ακμών, το μερικό υπεργράφημα από το $J$ είναι το υπεργράφημα:

Δοθέντος ενός υποσυνόλου $A\subseteq X$, το τμηματικό υπεργράφημα με σύνολο κορυφών το $A$ είναι το μερικό υπεργράφημα:

Το δυϊκό $H^{*}$ του $H$ είναι το υπεργράφημα του οποίου τα σύνολα κορυφών και ακμών έχουν αντισταφεί, έτσι ώστε οι κορυφές δίνονται από το $\{e_i\}$ και οι ακμές από το $\{X_m\}$, όπου:

Ο τελεστής του 'δυϊκού' υπεργραφήματος είναι ενελκτικός, δηλαδή $(H^{*}{)}^{*}=H$.

Ένα συνεκτικό γράφημα $G$ με σύνολο κορυφών το σύνολο κορυφών ενός συνεκτικού υπεργραφήματος $H$ λέγεται γράφημα-υποδοχέας για το $H$ εάν κάθε υπερακμή του $H$ ενάγει ένα συνεκτικό υπογράφημα στο $G$. Για μη συνεκτικό υπεργράφημα $H$, το $G$ είναι γράφημα-υποδοχέας εάν υπάρχει αμφιμονοσήμαντη απεικόνιση μεταξύ των συνεκτικών συνιστωσών των $G$ και $H$, έτσι ώστε κάθε συνεκτική συνιστώσα $G^{\prime }$ του $G$ είναι γράφημα-υποδοχέας για την αντίστοιχη συνιστώσα $H^{\prime }$ στο $H$.

Η κλίκα ενός υπεργραφήματος είναι το γράφημα με κορυφές τις κορυφές του υπεργραφήματος, και ακμές όλα τα ζεύγη κορυφών που βρίσκονται στην ίδια υπερακμή.

Πίνακες πρόσπτωσης

Έστω $V=\{v_1,\cdots ,v_n\}$ και $E=\{e_1,\cdots ,e_m\}$ τα σύνολα κορυφών και ακμών αντίστοιχα ενός υπεργραφήματος $H=(V,E)$. Για κάθε τέτοιο υπεργράφημα, ορίζεται ένας $n\times m$ πίνακας προσπτώσεων.

Για την περίπτωση των μη κατευθυνόμενων υπεργραφημάτων, ορίζεται πίνακας $I=(b_{i,j})$ όπου:

Ο ανάστροφος πίνακας $I^T$ του πίνακα προσπτώσεων είναι ουσιαστικά ο πίνακας του δυϊκού υπεργραφήματος $H^{*}=(V^{*},E^{*})$. Για κάθε $v_j^{*}\in V^{*}$ και $e_i^{*}\in E^{*}$ αληθεύει $u_j^{*}\in e_i^{*}$ αν και μόνο αν $b_{i,j}=1$.

Για την περίπτωση των κατευθυνόμενων υπεργραφημάτων, συμβολίζουμε με $H(e_j)$ το σύνολο των περάτων της ακμής $e_j$, με $T(e_j)$ το σύνολο των αρχών της, και ο πίνακας προσπτώσεων $I=(b_{i,j})$ ορίζεται:

Γράφημα προσπτώσεων

Ένα υπεργράφημα $H=(V,E)$ μπορεί να αναπαρασταθεί μέσω ενός διμερούς γραφήματος ως εξής: τα σύνολα $V$ και $E$ του υπεργραφήματος είναι τα μέρη του διμερούς γραφήματος, και τα $v_i,e_j$ συνδέονται με ακμή αν και μόνο αν $v_i\in e_j$. Αυτό το διμερές γράφημα ονομάζεται γράφημα προσπτώσεων.

Είναι φανερό ότι ένα διμερές γράφημα το οποίο δεν αφήνει ασύνδετη καμμία κορυφή ενός μέρους, μπορεί να ορίσει (μέσω της αντίστοφης διαδικασίας που αναφέραμε παραπάνω) ένα υπεργράφημα.

Κύκλοι

Σε αντίθεση με τα συνήθη μη κατευθυνόμενα γραφήματα, στα οποία υπάρχει μια έννοια κυκλικών και άκυκλων γραφημάτων, στα υπεργραφήματα υπάρχουν πολλοί μη ισοδύναμοι ορισμοί ακυκλικότητας, οι οποίοι ουσιαστικά επεκτείνουν τον αντίστοιχο ορισμό των συνήθων γραφημάτων.

Ένας πρώτος ορισμός ακυκλικότητας δίνεται από τον Claude Berge. Ένα υπεργράφημα είναι Berge-άκυκλο αν το γράφημα προσπτώσεών του είναι άκυκλο. Αυτός ο ορισμός είναι πολύ περιοριστικός. Για παράδειγμα, εάν ένα υπεργράφημα έχει ένα ζεύγος κορυφών $v\ne v^{\prime }$και ένα ζεύγος ακμών $f\ne f^{\prime }$ έτσι ώστε $v,v^{\prime }\in f$ και $v,v^{\prime }\in f^{\prime }$, τότε είναι Berge-κυκλικό. H Berge-κυκλικότητα μπορεί να ελεγθεί σε γραμμικό χρόνο, μέσω του γραφήματος προσπτώσεων.

Μπορούμε να ορίσουμε έναν ασθενέστερο ορισμό ακυκλικότητας στα υπεργραφήματα, αυτό που μετέπειτα ονομάστηκε $\alpha -$ακυκλικότητα. Αυτός ο ορισμός ακυκλικότητας είναι ισοδύναμος με το υπεργράφημα να είναι σύμμορφο (conformal: Κάθε κλίκα του πρωταρχικού [primal] γραφήματος καλύπτεται από κάποια υπερακμή) και το πρωταρχικό γράφημα να είναι χορδικό. Είναι επίσης ισοδύναμος με την αναγωγή του υπεργραφήματος στο κενό γράφημα, μέσω του αλγορίθμου GYO (επίσης γνωστός ως αλγόριθμος του Graham).

Κανείς μπορεί να ελέγξει σε γραμμικό χρόνο αν ένα υπεργράφημα είναι $\alpha -$ακυκλικό.

Σημειώστε ότι η $\alpha -$ακυκλικότητα έχει την εξής μη αναμενόμενη ιδιότητα: Με πρόσθεση υπερακμών σε ένα $\alpha -$κυκλικό υπεργράφημα, μπορεί να προκύψει ένα $\alpha -$ακυκλικό υπεργράφημα - για παράδειγμα, με πρόσθεση μιας υπερακμής που περιέχει κάθε κορυφή του υπερφραφήματος, οδηγούμαστε πάντοτε σε $\alpha -$ακυκλικό υπεργράφημα. Με αυτό υπόψη, ο Ronald Fagin όρισε ισχυρότερες έννοιες ακυκλικότητας, τη $\beta -$ακυκλικότητα και τη $\gamma -$ακυκλικότητα. Μπορούμε να πούμε ότι η $\beta -$ακυκλικότητα προϋποθέτει όλα τα υπο-υπεργραφήματα να είναι $\alpha -$ακυκλικά - αυτός ο ορισμός είναι τελικά ισοδύναμος με έναν ορισμό που είχε προτύτερα δώσει ο Graham. Η $\gamma -$ακυκλικότητα είναι περισσότερο περιοριστική και σχετίζεται με τα διαγράμματα Bachman.

Τόσο η $\beta$ όσο και η $\gamma -$ακυκλικότητα μπορούν να ελεγθούν σε πολυωνυμικό χρόνο.

Οι τέσσερεις έννοιες ακυκλικότητας μεταξύ τους σχετίζονται: Η Berge-ακυκλικότητα εξασφαλίζει την $\gamma -$ακυκλικότητα, η $\gamma$ την $\beta$, και η $\beta$ την $\alpha$. Καμία από την αντίστροφες συνεπαγωγές δεν ισχύει, το οποίο καθιστά τις τέσσερεις έννοιες ακυκλικότητας διαφορετικές.

Ισομορφισμοί, συμμετρίες και ισότητα

(Εκκρεμμεί η μετάφραση)

Ξενόγλωσσες σελίδες του ίδιου λήμματος

Το παρόν λήμμα αποτελεί μετάφραση του αντίστοιχου αγγλικού: hypergraph. Έχουν υπάρξει μερικές προσθήκες στο ελληνικό.

Δείτε επίσης

• Θεωρία γραφημάτων
• Πολυγράφημα
• Συνδιαστικός σχεδιασμός

Βιβλιογραφία

• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Springer
• Πρότυπο:Cite book
• Πρότυπο:Cite book
• Πρότυπο:Cite book